Polyhedral Discretizations for Elliptic PDEs

Junyu Liu, Daniele Panozzo, Mario Bostch, Teseo Schneider

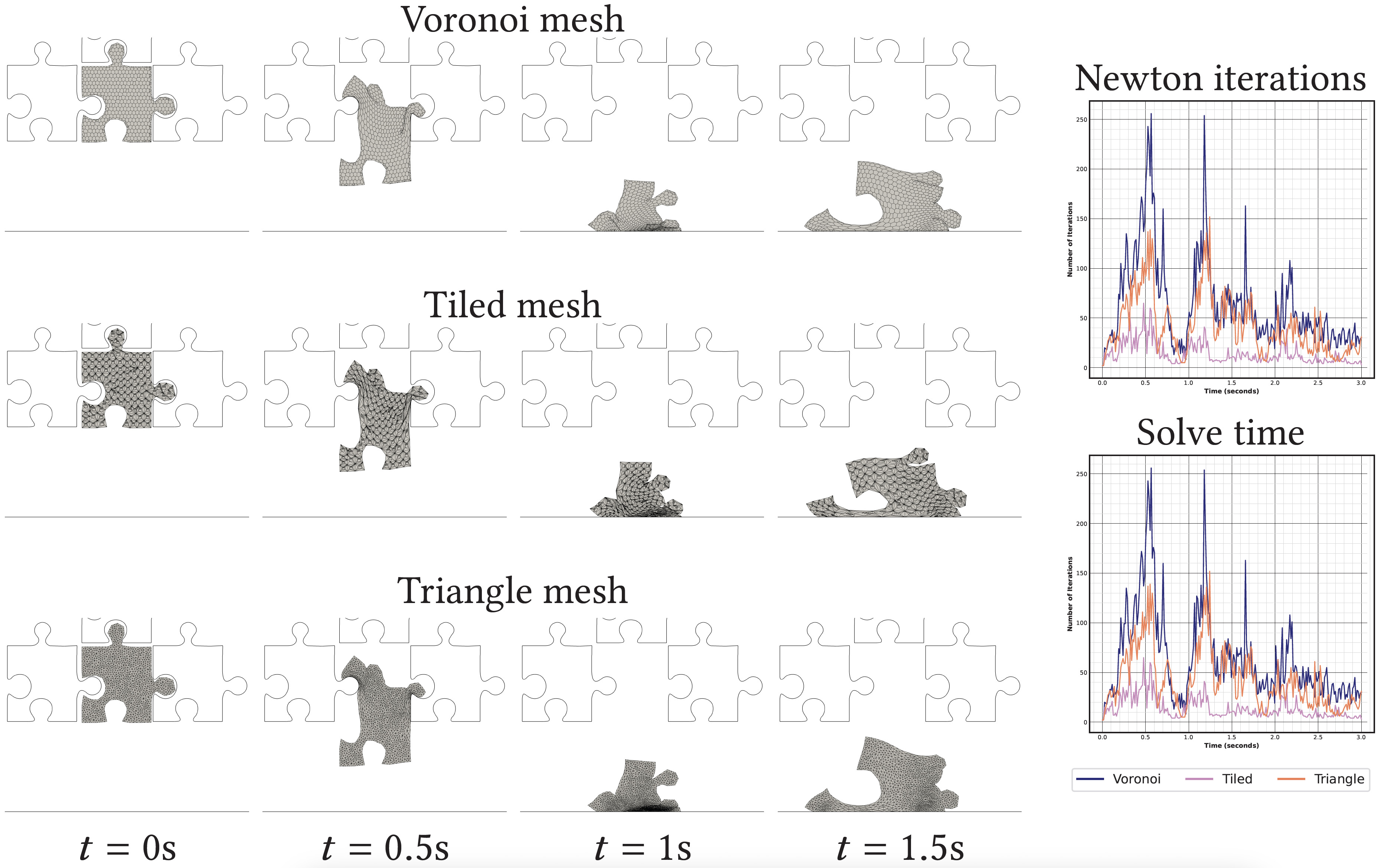
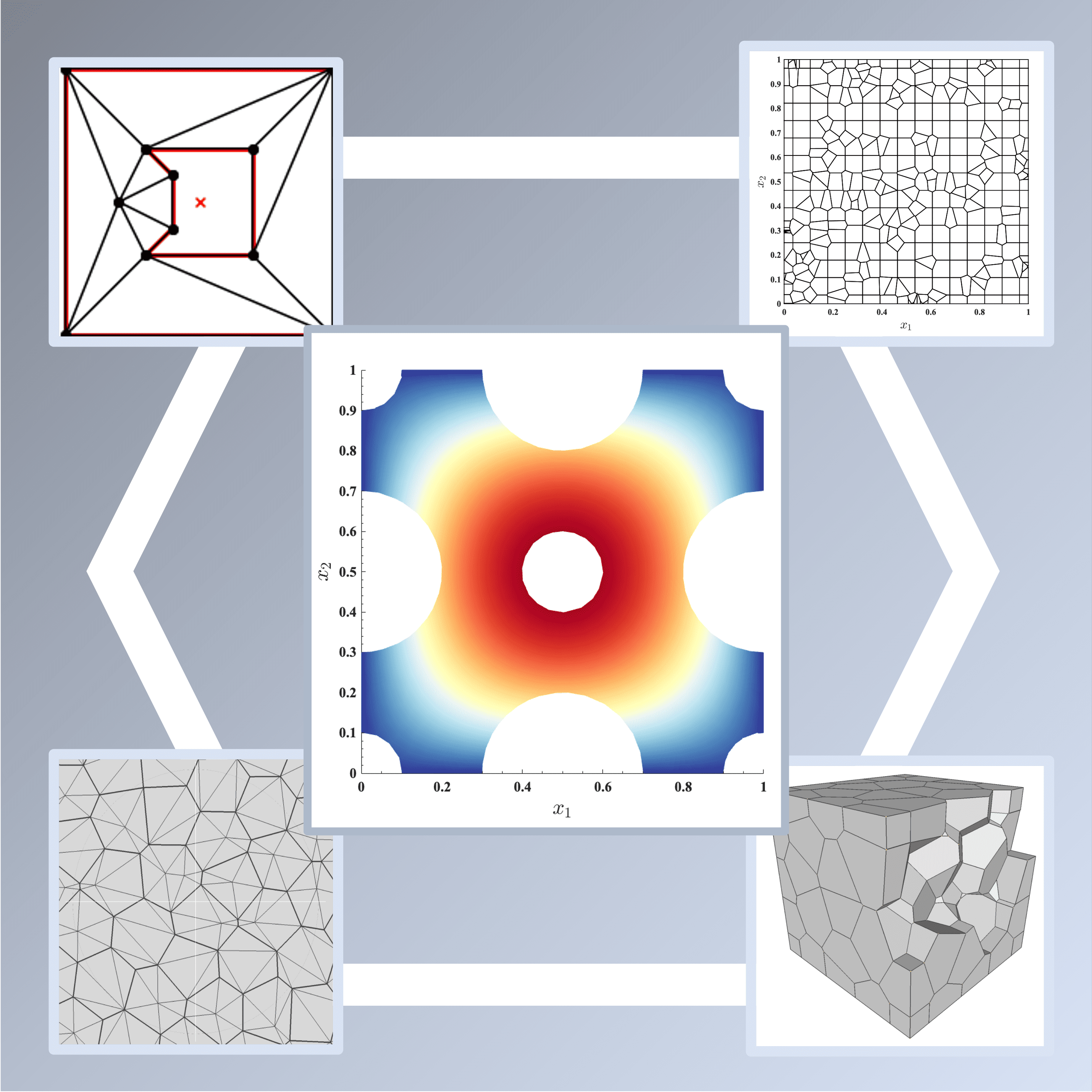
We study the use of polyhedral discretizations for the solution of heat diffusion and elastodynamic problems in computer graphics. Polyhedral meshes are more natural for certain applications than pure triangular or quadrilateral meshes, which thus received significant interest as an alternative representation. We consider finite element methods using barycentric coordinates as basis functions and the modern virtual finite element approach. We evaluate them on a suite of classical graphics problems to understand their benefits and limitations compared to standard techniques on simplicial discretizations. Our analysis provides recommendations and a benchmark for developing polyhedral meshing techniques and corresponding analysis techniques.